第四节 秩相关
参数法中介绍的直线相关只适用于正态双变量资料,但实际资料有时不能满足这些条件。如两事物有相关,但其观测结果不是计量资料而是等级资料,此时即可用秩相关来表达和分析。
本节介绍常用的Spearman秩相关。今以例10.8介绍其一般计算步骤:
1.将资料列成便于计算用的表,见表10.10,为便于编秩号,在列表时可按资料中一个变量的原始数据由小到大排队,但另一变量中各相应数值必须随成对关系变动,不能打乱。
2.两变量各自从小到大编秩号,同一变量数值相等时求平均秩号,见表10.10中的“秩号”栏。
3.求各对变量值秩号之差数d,再求∑d2。
4.代入式10.11,计算秩相关系数ra(又称Spearman秩相关系数)
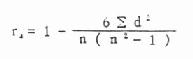
(10.11)
式中n为变量值的对子数。算得的r8与直线相关系数的意义相同,其范围在-1~+1之间,也分为正相关和负相关。
5.查表作结论
当n>50时,秩相关系数显著性的界值与直线相关系数相近似,故可根据ν=n-2查附表11来作判断:当n≤50时,则查阅附表16。
例10.8 通过普查得到七个地区居民中单纯性甲状腺肿患者百分比与当地食物、水中的含磺量如表10.10右侧第一、第三两栏所列。问该两事物是否显著相关?
表10.10 单纯性甲状腺肿患者百分数
与当地食物水中含碘量的秩相关分析
| 含 碘 量 | 患者百分数 | 秩号差d | d2 | ||
| X1 | 秩号 | X2 | 秩号 | ||
| 71 | 1 | 16.9 | 7 | -6 | 36 |
| 81 | 2 | 4.4 | 6 | -4 | 16 |
| 126 | 3 | 2.5 | 5 | -2 | 4 |
| 154 | 4 | 0.8 | 3 | 1 | 1 |
| 155 | 5 | 1.1 | 4 | 1 | 1 |
| 178 | 6 | 0.6 | 2 | 4 | 16 |
| 201 | 7 | 0.2 | 1 | 6 | 36 |
n=7∑d2=110
将n,∑d2代入式10.11得:
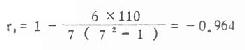
本例n=7,查例表16,得r80.05,7=0.786,r8 0.01,7=0.929,今∣r8∣>r80.01,7故P<0.01,α=0.01水准上拒绝H0,接受H1,故某地居民单纯性甲状腺肿患者百分数与当地食物、水中含碘量之间呈显著的负相关。
猜您喜欢
推荐典籍
