计算公式索引
相对数
公式(3.1)

公式(3.2)

公式(3.3)
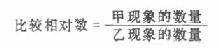
χ2检验
公式(3.4)理论频数
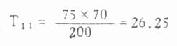
公式(3.5)χ2基本公式
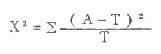
公式(3.6)χ2自由度 ν=(R-1)(C-1)
公式(3.7)χ2校正的基本公式
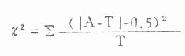
公式(3.8)四格表专用公式
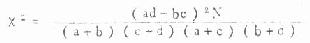
公式(3.9)四格表校正公式
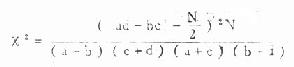
公式(3.10)2×k表专用公式
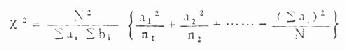
公式(3.11)
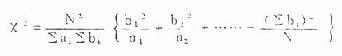
公式(3.12)R×C表通用公式
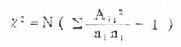
中位数
公式(4.1)当n为奇数时
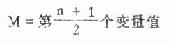
公式(4.2)当n为偶数时

公式(4.3)频数表上计算
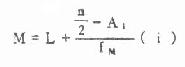
公式(4.4)
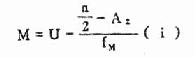
百分位数
公式(4.5)频数表上计算
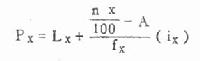
算术均数
公式(4.6) χ=(1/n)∑X
公式(4.7) χ=C+(1/n)(Xi-C)
公式(4.8) χa=Xa-1+(1/n)(Xa-Xa-1)
公式(4.9) χ=(1/n)∑fX
几何均数
公式(4.10)
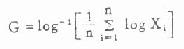
公式(4.11)
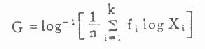
四分位数间距
公式(4.12) Q=P75-P25
均差
公式(4.13)
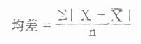
标准差
公式(4.14) 样本标准差
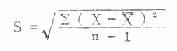
公式(4.15) 递推计算
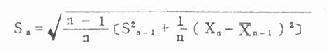
公式(4.16) 直接计算
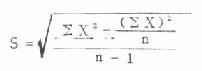
公式(4.17)
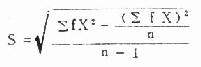
变异系数
公式(4.18) CV=S/X×100%, X>0
正态曲线
公式(5.1) 正态曲线方程
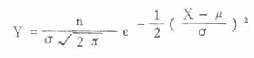
(5.2) 正态离差
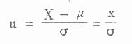
(5.3) 标准正态曲线
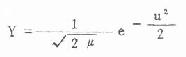
(5.4) 正常值范围 X±uαs
标准误
(6.1) 理论标准误
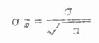
(6.2) 样本均数的标准误
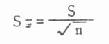
(6.3) 率的标准误

(6.4)
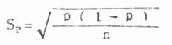
t分布
(6.5)
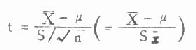
总体均数的估计
(6.6) 95%可信区间 X-t0.05,νSχ<μ<X+T0.05,ν Sχ
(6.7) 99%可信区间 X-t0.01,ν Sχ<μ<X+T0.01,ν Sχ
总体率的估计
(6.8) 95%可信区间P-1.96Sp<π<P+1.96SP<p
(6.9) 99%可信区间P-2.58Sp<π<P+2.58SP<p
t检验
公式(6.5)样本均数与总体均数比较
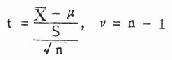
公式(7.1) 两样本均数比较的自由度 ν=n1+n2-2
公式(7.2) 合并方差
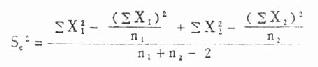
公式(7.3) 两均数相差的标准误
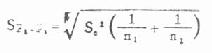
公式(7.4) t检验
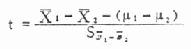
u检验
公式(7.5)两均数相关的标准误
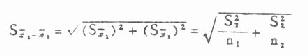
u检验
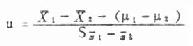
公式(7.6)两样本率比较
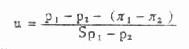
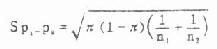
公式(7.7)
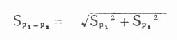
公式(6.4)
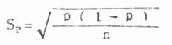
正态性检验
公式(7.8) w检验
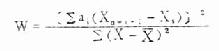
公式(7.9) 偏度系数
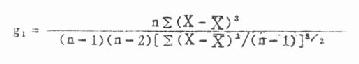
公式(7.10)
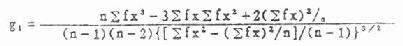
公式(7.11) 峰度系数
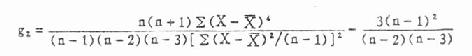
公式(7.12)
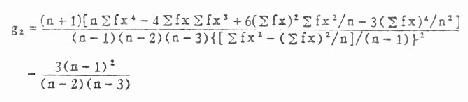
公式 (7.13) g1的抽样误差
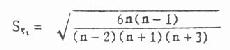
公式 (7.14) g2的抽样误差
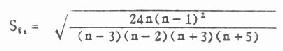
公式 (7.15) g1的u检验 u1=g1/Sg1
公式 (7.16) g2的u检验 u2=g2/Sg2
两方差齐性检验
公式(7.17) F=S12/S22,S1>S2
方差分析
公式(8.1) 总离均差平方和
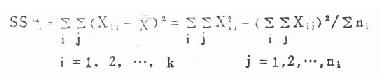
公式(8.2) 组间离均差平方和
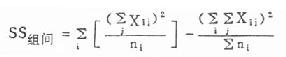
公式(8.3) 组内离均差平方和
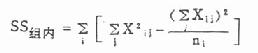
公式(8.4) 总变异自由度 ν总=N-1
公式(8.5)组间变异自由度 ν组间=k-1
公式(8.6) 组内变异自由度 ν组内=N-k
公式(8.7) F检验F=组间均方/组内均方
多个均数间两两比较
公式(8.8) 最小显著相差Dα=t,νS
A-
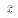
B
公式(8.9) 两均数的标准误
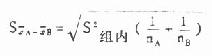
公式(8.10) 平均例数
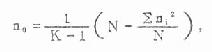
i=1,2,…,k
公式(8.11) 标准误
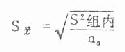
多个方差齐性检验
公式(8.12)
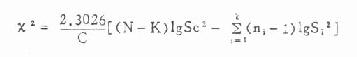
公式(8.13)
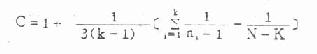
直线相关
公式(9.1) 直线相关系数
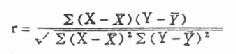
公式(9.2) 离均差积和
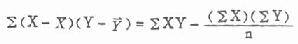
公式(9.3) 相关系数t检验
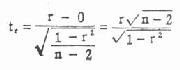
直线回归
公式(9.4) 直线回归方程 γ=a+bx
公式(9.5) 回归系数
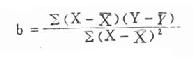
公式(9.6) 截距 a=γ-bχ
公式(9.7) 回归系数t检验
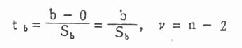
公式(9.8) 回归系数的标准误
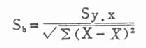
公式(9.9) 标准估计误差
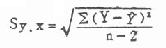
公式(9.10) 估计误差平方和
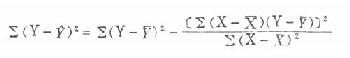
公式(9.11) 两回归系数相关的t检验
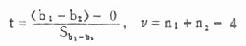
公式(9.12) 两回归系数相差的标准误
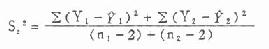
公式(9.13) 两回归系数的合并方差
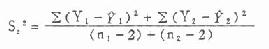
符号检验
公式(10.1) 成对资料比较
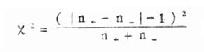
,ν=1
公式(10.2) 秩号的中位数

公式(10.3) 两组符号检验
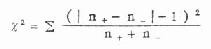
,ν=1
公式(10.4) 两组符号检验
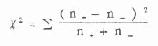
,ν=组数-1
秩和检验
公式(10.6) 成对资料比较
公式(10.6) 两组资料求较小R'R'=n1(n1+n2+1)-R
公式(10.7)两组资料比较
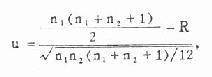
公式(10.8) 多组完全随机设计资料的比较
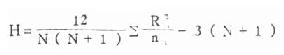
公式(10.9) 多组随机单位组设计资料的比较
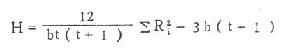
公式(10.10) 多组秩和的两两比较
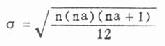
秩相关系数
公式(10.11)Spearman秩相关系数
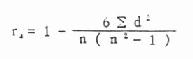
参照单位分析
公式(10.12) 平均R值
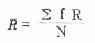
公式(10.13)R的标准误
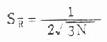
公式(10.14) R的95%可信限
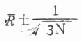
样本含量的估计
公式(11.1) 两个率比较所需例数
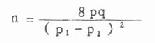
,1-β=0.5,α=0.05
公式(11.2) 大样本成对资料比较均数所需例数 n=4S2/X2,1-β=0.5,α=0.05
公式(11.3) 小样本成对资料比较均数所需例数
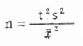
,1-β=0.5
